如果这篇博客帮助到你,可以请我喝一杯咖啡~
CC BY 4.0 (除特别声明或转载文章外)
这是41616在做题的时候自主发现的一个小结论,在考场上不能直接用,但是挺有意思的。
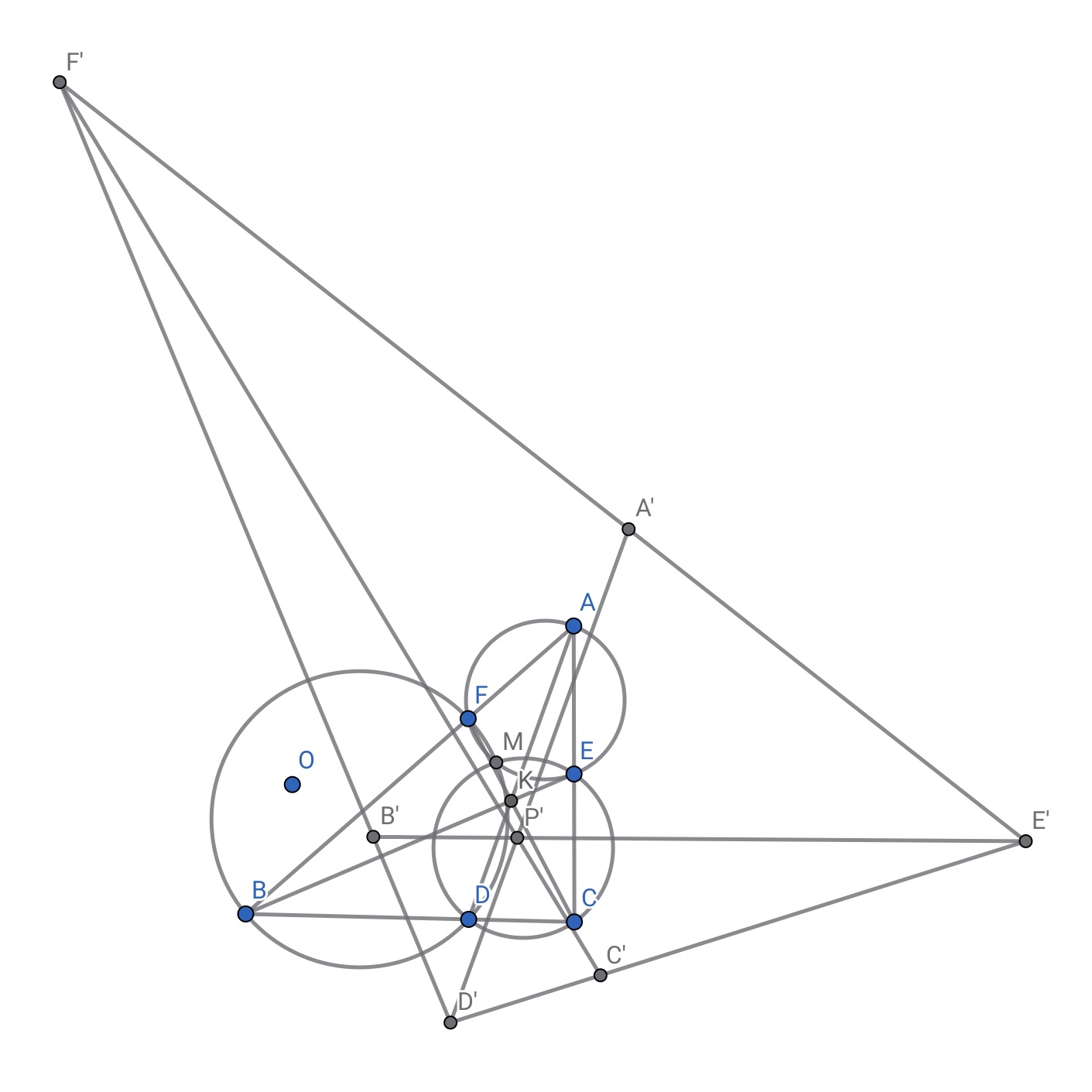
定理叙述:$\triangle ABC$的边$BC$、$CA$、$AB$上各有一个点$D$、$E$、$F$,$\odot AEF$、$\odot BDF$、$\odot CDE$交于一个点$M$(易知这三个圆有一个公共点),则$AD$、$BE$、$CF$三线共点的充要条件是$\odot AMD$、$\odot BME$、$\odot CMF$共轴。(共轴的意思是这三个圆两两的根轴均重合)
证明:把整个图以点$M$为反演中心,$1$为反演半径作反演,每个点的反演像用这个点的名称后面加上一个$’$来表示。则:
$\blacktriangleright AD$、$BE$、$CF$三线共点$\Leftrightarrow\dfrac{BD}{DC}\cdot\dfrac{CE}{EA}\cdot\dfrac{AF}{FB}=1$;
$\blacktriangleright\odot AMD$、$\odot BME$、$\odot CMF$共轴$\Leftrightarrow A’D’$、$B’E’$、$C’F’$三线共点$\Leftrightarrow\dfrac{B’D’}{D’C’}\cdot\dfrac{C’E’}{E’A’}\cdot\dfrac{A’F’}{F’B’}=1$。
注意到$\triangle MBD\sim\triangle MD’B’$,于是有$\dfrac{MB}{MD’}=\dfrac{BD}{D’B’}$,即:
$\dfrac{BD}{MB}=\dfrac{B’D’}{MD’}①$
同理有如下五式:
$\dfrac{DC}{MC}=\dfrac{D’C’}{MD’}②$
$\dfrac{CE}{MC}=\dfrac{C’E’}{ME’}③$
$\dfrac{EA}{MA}=\dfrac{E’A’}{ME’}④$
$\dfrac{AF}{MA}=\dfrac{A’F’}{MF’}⑤$
$\dfrac{FB}{MB}=\dfrac{F’B’}{MF’}⑥$
$\dfrac{①}{②}\times\dfrac{③}{④}\times\dfrac{⑤}{⑥}$,得:$\dfrac{BD}{DC}\cdot\dfrac{CE}{EA}\cdot\dfrac{AF}{FB}=\dfrac{B’D’}{D’C’}\cdot\dfrac{C’E’}{E’A’}\cdot\dfrac{A’F’}{F’B’}$,结合两个“$\blacktriangleright$”即得证。