如果这篇博客帮助到你,可以请我喝一杯咖啡~
CC BY 4.0 (除特别声明或转载文章外)
原题:$\triangle ABC$为内接于$\odot O$的锐角三角形,过$A$作$AD//BC$交$\odot O$于另一点$D$,类似定义$E$、$F$。$\triangle ABC$的垂心为$H$,$\triangle DEF$的内心为$I$。证明:$O$为$HI$中点。
证明:
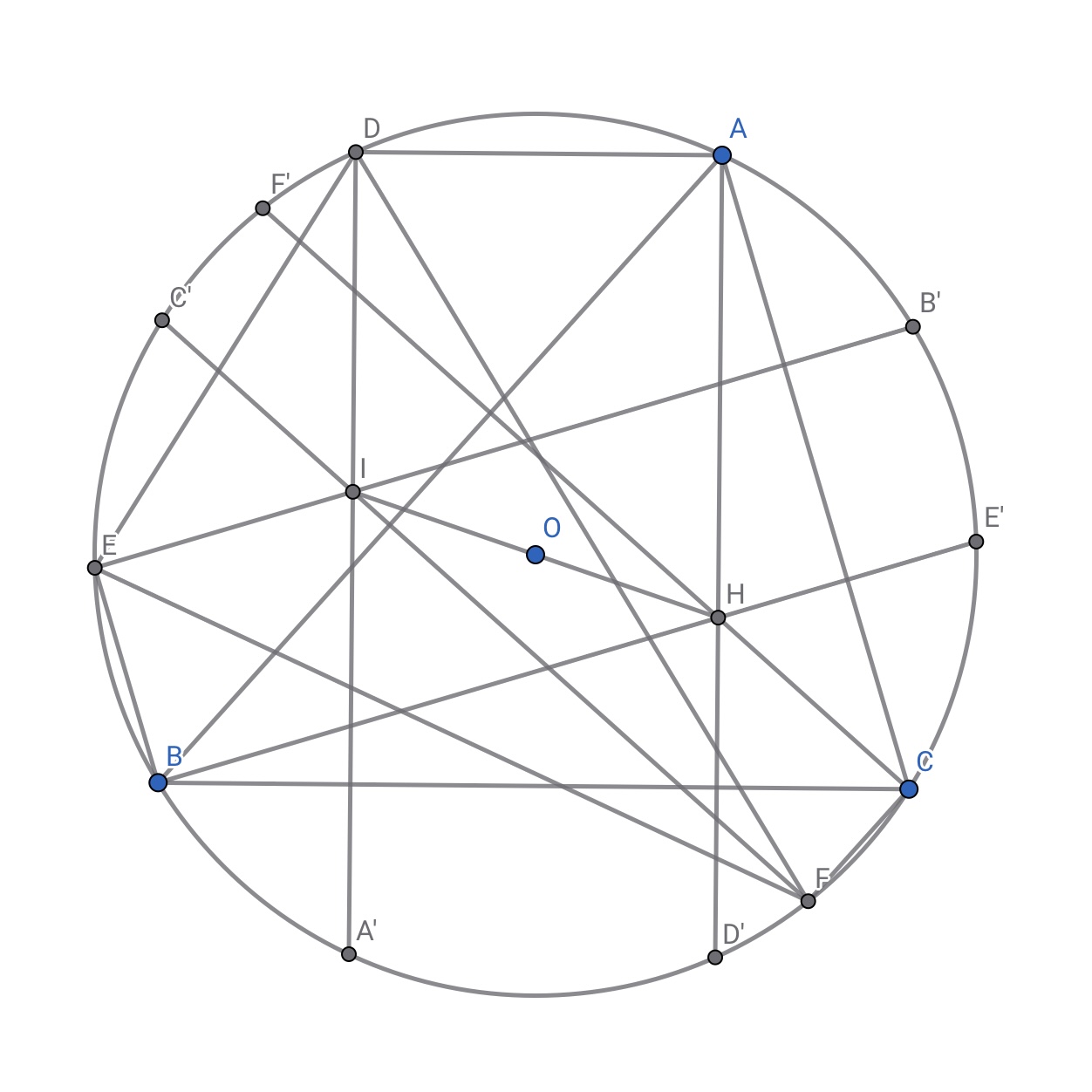
$\blacktriangleright$辅助线:把$A\sim F$这六个点关于$\odot O$的对径点取出来,分别叫$A’\sim F’$。
$\blacktriangleright$Step 1:由于$AD//BC$,$AD\bot AD’$,所以$AD’\bot BC$,$AD’$过$H$。同理,$BE’$、$CF’$也过$H$,$H$是$AD’$、$BE’$、$CF’$的交点。
$\blacktriangleright$Step 2:由于$\overgroup{AF}=\overgroup{BC}=\overgroup{AE}$,所以$A’$是$\overgroup{EF}$的中点,$A’D$过$I$。同理,$B’E$、$C’F$也过$I$,$I$是$A’D$、$B’E$、$C’F$的交点。
$\blacktriangleright$Step 3:因为$A’\sim F’$取的都是对径点,所以$AD’$与$A’D$、$BE’$与$B’E$、$CF’$与$C’F$分别关于点$O$对称。因此,点$H$和点$I$也关于点$O$对称,即$O$为$HI$中点。